Riflessione rispetto a un piano arbitrario
Un piano nello spazio ha un'equazione cartesiana della forma
![]() , con
, con
![]() non tutti nulli. Il vettore
non tutti nulli. Il vettore
![]() è normale (cioè ortogonale) al piano. L'equazione del piano
è normale (cioè ortogonale) al piano. L'equazione del piano
![]() passante per il punto
passante per il punto
![]() e con direzione normale (
e con direzione normale (
![]() ) è dunque
) è dunque
![]() .
.
Per ottenere la riflessione rispetto al piano
![]() , è sufficiente trasformare il piano in un piano coordinato, ad esempio il piano
, è sufficiente trasformare il piano in un piano coordinato, ad esempio il piano
![]() . Si può procedere come nella sezione precedente, traslando
. Si può procedere come nella sezione precedente, traslando
![]() nell'origine e ruotando il vettore normale (
nell'origine e ruotando il vettore normale (
![]() ) con angoli
) con angoli
![]() e
e
![]() in modo da renderlo parallelo all'asse
in modo da renderlo parallelo all'asse
![]() . La riflessione è data quindi dalla concatenazione
. La riflessione è data quindi dalla concatenazione
![]()
Esempio:
consideriamo il piano
![]() , passante per il punto
, passante per il punto
![]() . Il vettore normale
. Il vettore normale
![]() ha lunghezza 3 e quindi
ha lunghezza 3 e quindi
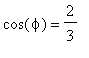 ,
,
 , c
, c
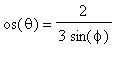 =
=
![]() ,
,
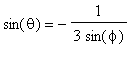 =
=
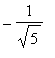 .
.
matrice..