4.2 Proiezioni dello spazio
Passiamo ora a descrivere le proiezioni dello spazio tridimensionale su un piano. Sia
![]() il vettore delle coordinate omogenee del piano di proiezione (il piano di vista) e sia
il vettore delle coordinate omogenee del piano di proiezione (il piano di vista) e sia
![]() un punto esterno al piano. La
proiezione
da
un punto esterno al piano. La
proiezione
da
![]() sul piano
sul piano
![]() è la trasformazione
è la trasformazione
![]() che applica un punto
che applica un punto
![]() , distinto da
, distinto da
![]() , nel punto
, nel punto
![]() del piano di vista che si ottiene intersecando il piano con la retta per
del piano di vista che si ottiene intersecando il piano con la retta per
![]() e
e
![]() . Se
. Se
![]() appartiene al piano per
appartiene al piano per
![]() parallelo al piano di vista,
parallelo al piano di vista,
![]() è il punto all'infinito nella direzione della retta per
è il punto all'infinito nella direzione della retta per
![]() e
e
![]() . Se
. Se
![]() è un punto improprio, la proiezione è
parallela
(con direzione delle rette di proiezione data da
è un punto improprio, la proiezione è
parallela
(con direzione delle rette di proiezione data da
![]() ), altrimenti è detta
centrale
o
proiezione
prospettica
.
), altrimenti è detta
centrale
o
proiezione
prospettica
.
Ricaviamo la matrice della proiezione:
i punti della retta per
![]() e
e
![]() hanno coordinate omogenee della forma
hanno coordinate omogenee della forma
![]() (vedi la sezione 3.3) e l'intersezione
(vedi la sezione 3.3) e l'intersezione
![]() tra tale retta e il piano di vista è caratterizzata dalla condizione
tra tale retta e il piano di vista è caratterizzata dalla condizione
![]() cioé
cioé
![]()
Scegliendo
![]() e
e
![]() si ottiene
si ottiene
![]()
![]() =
=
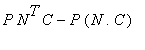 =
=
![P*(N^T*C-N.C*I[4])](images/geo859.gif)
Dunque
![]() , con
, con
![M = N^T*C-N.C*I[4]](images/geo861.gif) .
.
Come nel caso bidimensionale, le proiezioni sono esempi di trasformazioni proiettive dello spazio. Le proiezioni centrali non sono trasformazioni affini, diversamente da quelle parallele. Una conseguenza del fatto che una proiezione parallela trasforma punti impropri in punti impropri, è la seguente proprietà: ogni coppia di rette parallele viene trasformata da una proiezione parallela in una coppia di rette ancora parallele (le due rette devono incontrarsi ancora in un punto improprio).
Esempio 1:
la proiezione parallela sul piano
![]() in direzione parallela all'asse
in direzione parallela all'asse
![]() ha matrice
ha matrice
![M = matrix([[0], [0], [1], [0]])*matrix([[0, 0, 1, ...](images/geo864.gif) =
=
![matrix([[-1, 0, 0, 0], [0, -1, 0, 0], [0, 0, 0, 0],...](images/geo865.gif)
poiché il piano di vista
![]() ha equazione omogenea
ha equazione omogenea
![]() e vettore delle coordinate omogenee
e vettore delle coordinate omogenee
![]() e il centro (punto improprio) ha coordinate omogenee
e il centro (punto improprio) ha coordinate omogenee
![]() . Naturalmente, la proiezione associa al punto di coordinate cartesiane (
. Naturalmente, la proiezione associa al punto di coordinate cartesiane (
![]() ) il punto di coordinate omogenee
) il punto di coordinate omogenee
![]() e di coordinate cartesiane (
e di coordinate cartesiane (
![]() ).
).
Esempio 2:
la proiezione centrale sul piano
![]() dal punto di vista (
dal punto di vista (
![]() ) ha matrice
) ha matrice
![M = matrix([[0], [0], [1], [0]])*matrix([[1, 5, 3, ...](images/geo875.gif) =
=
![matrix([[-3, 0, 0, 0], [0, -3, 0, 0], [1, 5, 0, 1],...](images/geo876.gif)
Dunque la trasformazione associa al punto di coordinate cartesiane (
![]() ) il punto di coordinate omogenee
) il punto di coordinate omogenee
![]() e di coordinate cartesiane
e di coordinate cartesiane
![[(-3*x+z)/(z-3), (-3*y+5*z)/(z-3), 0]](images/geo879.gif) . Si noti che nel caso di trasformazioni proiettive che non sono affini, le coordinate cartesiane del punto trasformato si esprimono mediante quozienti di espressioni di primo grado nelle coordinate
. Si noti che nel caso di trasformazioni proiettive che non sono affini, le coordinate cartesiane del punto trasformato si esprimono mediante quozienti di espressioni di primo grado nelle coordinate
![]() .
.
Esempi