Esempio:

Definiamo una proiezione 'cabinet' sul piano . Il vettore normale è . Se è la direzione di proiezione, si ottiene una proiezione 'cabinet' quando

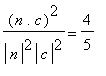(deve essere 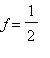; vedi l'esercizio sopra e il suggerimento)

Dunque la condizione sulla direzione diventa

ovvero

Una possibile direzione è , corrispondente alla matrice di proiezione

> MP([0,0,1,0],[3,4,10,0]);

> colore:=[red,green,blue,white,black,yellow]:

> vertici:=[[1,2,4,3],[1,2,6,5],[1,3,7,5],[2,4,8,6],[3,4,8,7],[5,6,8,7]]:

> box:= proc(l) local i,ll; global faccia6; ll:=convert(l,listlist):for i from 1 to 6 do faccia6[i]:=polygon([seq(ll[vertici[i,j]],j=1..4)],color=colore[i]) od; RETURN(convert(faccia6,set)) end:

> c0:=[[0,0,0],[1,0,0],[0,1,0],[1,1,0],[0,0,1],[1,0,1],[0,1,1],[1,1,1]];

> c1:=trasforma(c0,MP([0,0,1,0],[3,4,10,0])); proiezione 'cabinet' del cubo unitario c0 sul piano

> disegno3d(box(c0) union box(c1));

> c2:=trasforma(c0,MP([0,0,1,0],[3,4,5,0])); proiezione cavaliera di c0 sul piano

> disegno3d(box(c2));

>