Esempio:

Riprendiamo l'esempio in 4.4: consideriamo la proiezione prospettica sul piano dal punto (1,5,3), con il sistema di coordinate del piano di vista avente origine , direzione del primo asse (3,4,0) e direzione del secondo asse (-4,3,0) .

Siano rispettivamente (-3,-3) e (3,2) gli angoli inferiore sinistro e superiore destro della finestra nel piano di vista, e siano (500,400) e (980,700) gli angoli della finestra sul dispositivo grafico (ad esempio, uno schermo con risoluzione 1280x1024). La matrice è il prodotto

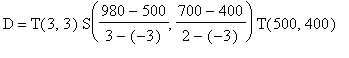
> d := evalm(T(3,3)&*S((980-500)/(3-(-3)),(700-400)/(2-(-3)))&*T(500,400));

> t:=trasforma(t2d,d); applichiamo la trasformazione al tetraedro t0 proiettato (cf. 4.2 e 4.4)

> plots[display](tetraedro(t),scaling=CONSTRAINED,view=[500..980,400..700],axes=BOXED);

> Vp:=evalm(MP([0,0,1,0],[1,5,3,1])&*Kd([1,2,0],[3,4,0],[-4,3,0])&*d); questa è la matrice complessiva che rappresenta la 'viewing pipeline'

> trasforma(t0,Vp);

> c:=trasforma(c0,Vp): la 'viewing pipeline' applicata al cubo unitario c0

> plots[display](box(c),scaling=CONSTRAINED,view=[500..980,400..700],axes=BOXED);

>