Rotazione con asse arbitrario

Se l'asse di rotazione non è un asse coordinato, la rotazione può essere ottenuta trasformando l'asse di rotazione in uno degli assi coordinati, per esempio l'asse , applicando poi la rotazione primaria attorno all'asse , e infine componendo con la trasformazione che riporta l'asse nell'asse di rotazione.

Si noti che per definire il verso della rotazione attorno all'asse, è necessario fissare un orientamento lungo l'asse di rotazione (esattamente come per gli assi coordinati). Questo può essere fatto scegliendo un vettore direzione per l'asse di rotazione.

Sia dunque l'asse di rotazione, passante per un punto e con direzione un vettore che possiamo supporre unitario: = 1. Il vettore definisce un punto sulla sfera di raggio1 centrata nell'origine. Sulla sfera è possibile introdurre due coordinate sferiche , la longitudine e la colatitudine , che sono rispettivamente l'angolo tra l'asse e la proiezione ortogonale di sul piano e l'angolo tra l'asse e il vettore .

La proiezione di sul piano ha lunghezza e dunque e . Inoltre .

La concatenazione

trasforma l'asse di rotazione nell'asse , poiché porta il punto nell'origine e il vettore direzione nel vettore ( ). Per ottenere la rotazione di un angolo attorno alla retta orientata basta concatenare le seguenti trasformazioni

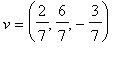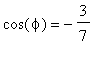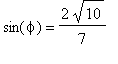Esempio: sia la retta passante per i punti e , orientata secondo il vettore direzione . Il vettore ha lunghezza e quindi . Dunque e (la colatitudine è compresa tra 0 e , con seno positivo) e 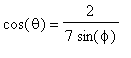, , 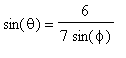cioè , .

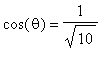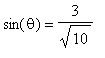matrice..