4.3.1 Proiezioni parallele

Le proiezioni dello spazio alterano le distanze tra i punti. In generale, il rapporto tra la lunghezza del segmento proiettato e la lunghezza del segmento originale è differente da 1. Tale rapporto dipende solo dalla direzione del segmento e per questo lo chiameremo fattore di scala nella direzione determinata da un vettore .

Il segmento con estremi e = ha lunghezza e viene trasformato dalla proiezione con matrice nel segmento i cui estremi hanno coordinate omogenee e . La quarta colonna di ha elementi ( ), per cui la quarta coordinata omogenea viene moltiplicata per . Ne deriva che il segmento proiettato ha lunghezza . Dunque il fattore di scala in direzione è

(1)

dipendente solo dalla direzione di .

Esercizio: Mostrare che per ogni proiezione parallela il fattore di scala in una direzione parallela al piano di vista è 1.

Esercizio: Mostrare che il fattore di scala in direzione perpendicolare al piano di vista è uguale a se, e solo se, l'angolo tra il piano di vista e la direzione di proiezione soddisfa la relazione

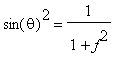ovvero

(Suggerimento: se è la direzione di proiezione, si ha . Si applichi la formula (1) con = e si ottenga )

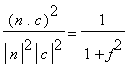Una proiezione parallela è detta ortogonale se la direzione di proiezione è perpendicolare al piano di vista. In tal caso, se il piano ha vettore omogeneo , il centro di proiezione è (o un qualsiasi suo multiplo non nullo).

Se la direzione della proiezione non è parallela a uno degli assi coordinati, solitamente la proiezione ortogonale è detta assonometrica . A loro volta tali proiezioni assonometriche si distinguono in isometriche, dimetriche e trimetriche, a seconda che 3, 2 o nessuno dei valori assoluti , , siano uguali tra di loro. Nel primo caso i fattori di scala nelle direzioni dei tre assi sono uguali, nel secondo sono uguali nelle direzioni di due assi.

Esercizio: Sia . Mostrare che il fattore di scala in direzione è , in direzione è , in direzione è .

Una proiezione parallela è obliqua se non è ortogonale. In particolare, si ottiene una proiezione cavaliera se l'angolo tra il piano di vista e la direzione di proiezione è . In questo caso i segmenti perpendicolari al piano di vista non cambiano lunghezza ( nell'esercizio visto sopra). Si ottiene invece una proiezione 'cabinet' se l'angolo è tale che 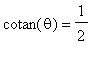, cioè se 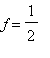(l'angolo è circa 1.1 radianti).

Esempio: