![M = N^T*C-N.C*I[4]](images/geo950.gif) la matrice che rappresenta la proiezione prospettica dal centro
la matrice che rappresenta la proiezione prospettica dal centro
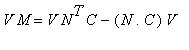 è zero, cioè se
è zero, cioè se
4.3.2 Proiezioni prospettiche
Sia
![M = N^T*C-N.C*I[4]](images/geo950.gif) la matrice che rappresenta la proiezione prospettica dal centro
la matrice che rappresenta la proiezione prospettica dal centro
![]() (con
(con
![]() ) sul piano
) sul piano
![]() . Sia
. Sia
![]() una direzione nello spazio, corrispondente al punto improprio
una direzione nello spazio, corrispondente al punto improprio
![]() . La proiezione di
. La proiezione di
![]() è ancora un punto improprio se la quarta componente del prodotto
è ancora un punto improprio se la quarta componente del prodotto
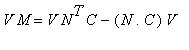 è zero, cioè se
è zero, cioè se
![]()
Ma
![]() e quindi la condizione diventa
e quindi la condizione diventa
![]() . Dunque la direzione
. Dunque la direzione
![]() deve essere perpendicolare alla normale
deve essere perpendicolare alla normale
![]() , cioè parallela al piano di vista. Questo fatto implica che le rette parallele che non sono parallele al piano di proiezione vengono proiettate in rette che convergono verso un punto del piano di proiezione, il
punto di fuga
, mentre le rette parallele al piano di proiezione restano parallele.
, cioè parallela al piano di vista. Questo fatto implica che le rette parallele che non sono parallele al piano di proiezione vengono proiettate in rette che convergono verso un punto del piano di proiezione, il
punto di fuga
, mentre le rette parallele al piano di proiezione restano parallele.
Il piano di proiezione può essere parallelo a nessuno, a uno o a due assi coordinati. Rispettivamente, si hanno 3,2,1 punti di fuga ( principali ) per le rette parallele agli assi coordinati.
Esempio